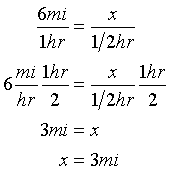Ann runs at a pace of 6 miles per hour. How many miles can she run in 30 minutes?

Ann runs at a pace of 6 miles per hour. How many miles can she run in 30 minutes?

Solution:

This is a proportion:

Solve the inequality and express the solution in interval form.

Solution:

For convenience we'll compare an appropriate expression to 0 instead of 1. Then we can find x-values of interest to determine where to shade (i.e. where the inequality is true).

 





















This graph shows our solution another way. Notice that we graph both sides of the inequality. Then we can actually see when the left side is greater...

Find the exact value of the remaining trigonometric functions if cosA= -3/5 and sinA < 0

Find the 11th term of the sequence 1,2,4,8,…

These terms are all powers of 2, so we can write:

Hyperbolic functions: find the inverse of arcsinh(x)

Factor 7x2-16x+4

Volume of similar cylinders

The cylinders shown are similar.

What is the volume of the larger cylinder?

Solution:

Evaluate the functions

Given: f(x) = x³ - 3x and g(x) = x² - 8. What is f(10) - g(10)?


Solution:

Find the inverse of the matrix (if there is one) algebraically.

Find the inverse of the matrix (if there is one) algebraically.  If there isn’t an inverse, say that the matrix is singular

[3 1 2]

[3 2 -1]

[1 1 1]

Two chords intersect with the measures shown in the drawing.

What is the value of x?

Solution:

we know that the product of the lengths of one intersecting chord must be equal to the product of the lengths of the other, so...

For what value of x is if the lines are parallel in this figure?

Solution:

We know that x and 40.03 are supplementary, so x+40.03=180. Therefore x=139.97 degrees

What is the solution set for the given equation? 3|x + 4| = 18

Let's try a different approach this time...

3|x + 4| = 18

has the same solution as

|x + 4| = 6


We look for the number(s) that can add/subtract to obtain 6. We can see that x=2 will work. No other positive number will work, however if we consider negative numbers then -10 seems possible. In fact is does work because |-10+4| = |-6| = 6. So x=-10.

What is the number of turning points in the graph of the function of x defined below?

y = 2x² + 5x - 7

Solution:

The polynomial y has degree n=2 so the maximum number of turns it can have is n-1 = 2-1 = 1. (In fact we know that our polynomial is a quadratic and it opens upwards so this is another way to know it only has one turn).

Find x.

What is the value of x?

Solution:


TV is a diameter, and SU is perpendicular to TV. This means that x=8

The polynomial equation x(x2+4)(x2-x-6)=0 has how many real roots?

Solution:

x2+4 contributes complex zeros. This means that the factors x and x2-x-6 contribute real zeros. Therefore the polynomial has 3 real zeros

What are the coordinates of the vertex of the graph of the function -2(x - 1)2 = y + 5?

so the vertex is (1,5)

If f(x) = 5x2 - 7, what is f(-3)?

Given quadrilateral KLMN, what is the value of x?

Given quadrilateral KLMN, what is the value of x?


Solution:

3x+x+25+80+95=360 (why?)

4x+200=360

4x=160

x=40

if tan(theta) = -3 and cos(theta) < 0, then tan(theta/2) = ?

so

so

 (we take the negative case because cosine is negative for this example)
now

Therefore...


which simplifies to

Evaluate the quotient (5 + i)/(1 + 3i)

Write 2 (1 + i) – 3(2-3i) in the form of a +bi

 

next we can write 

find the unknown length in the right triangle one side is 9m and the other side 15m.

If we assume that 15m is the longest side then a side of 12m will give us a right triangle (why?)

:)

What are the x-intercepts for the graph of y = x2 + 5x - 6?

We can use grouping to solve this quadratic because it can be factored.

x2+5x-6=0

x2 +6x-x-6=0

(x2+6x)-(x+6)=0

x(x+6)-(x+6)=0

(x-1)(x+6)=0

Next we can use the zero product property

x-1=0

x=1

or

x+6=0

x=-6

Solve the triangle: side a=3, side b=2, side c= 2.

One positive number is 5 times another number. The difference between the two numbers is 1352, find the numbers

1) y=5x
2) y-x=1352


then we can write

5x-x=1352
4x=1352
x=1352/4
x=338

so y=5(338)=1690

Find the inverse

Find the inverse of the 2x2 matrix below

[-3 1]
[-6 2]


Solution:

so our matrix is not invertible

Solve each right triangle A=35(degrees) and side a=5

Find exact value cos(2x) = 0 on the interval [0, 2pi]

simplify: 53-[3(8+2)+5(9-5)]

53-[3(8+2)+5(9-5)]=
53-[3(10)+5(4)]=
53-[30+20]=
53-50=3
:)

Find the solution set for the absolute value equation.

Find the solution set for the equation.

|x  - 7| = | 8 - x|

|x  - 7| = | 8 - x| 

means

x  - 7 =  8 - x  or   x - 7 = -8 + x (which has no solution)

we we can write

x + x - 7 - 8 = -x + x

2x -15 = 0

2x = 15

x = 15/2

find the slope of the linear equation y=3x-6

Since this equation is written in slope-intercept form, we can see that the slope is the coefficient of the x term. The slope is m=3

for the sequence,describe the pattern, write the next term, and write a rule for the nth term 1,2,4,8.

This sequence is the powers of 2, so the next term is 16 and the rule for the nth term is

notice we subtract 1 from n (why?)

:)

What is the solution to the radical equation?

  - 1 = 2

What is the inverse of the sentence, "If Sam leaves, then I will stay."?

The logical inverse of an if-then statement p -> q is

~p -> ~q

For us 

p is "if Sam leaves" so ~p is "If Sam does not leave"

and q is "I will stay" so ~q is "I will not stay"

Therefore the inverse is:

If Sam does not leave, then I will not stay.

The element lawrencium has a half-life of 10 hours. What fraction of 1 ounce of lawrencium will remain after 4 days 4 hours?

4 days and 4 hours is 4(24)+4 = 100 hours 
so our quantity is halved 10 times over the time period: 

 



so its 1/1024 oz

Determine Algebraically whether f(x) = 1 + x + x^2 is even, odd, or neither

A function is even if f(x) = f(-x), but for our function

f(-x)=1-x+x^2

so it is not even.

To be odd -f(x)=f(-x), and for our function

-f(x) = -1-x-x^2

and so it is also not odd.

Therefore it is neither.

Find the twentieth term of the arithmetic sequence with a1 = 15 and d = 4.

For an arithmetic progression we use the formula:

n=20, a1=15, d=4








:)

how can i decompose this partial fraction(4x^3)/(x^3-x^2)

This is not a "proper" decomposition problem. Typically the degree of the denominator is greater than the degree of the numerator...

but...we can still simplify...
notice that this expression can be factored:

from here we notice that by polynomial long division (don't know how to show using this editor) that:

so our expression simplifies to...



:)

find a if a(a-8)=20

a(a-8)=20

so a= 10 or a=-2

Is it a function?

given the relation {(-4,-2),(1,-4),(3,0),(4,3)} determine if this relation is a function
a. yes it is a function because each x value has only one y value
b. no it is not a function because -4 appears twice
c. no it is not a function because each x value does not have a unique y value
d. yes it is a function because each x value is unique

by definition of a function:
a. yes it is a function because each x value has only one y value

Write (2-2i)^8 in the standard form a+bi

Find area of triangle: a=2,b=1,theta=100(degrees) <--the angle between them

Find dy/dx at the point (0, 1), if y^5 = (x + 2)^4 + e^xln y − 15 Amy.