Sunday, March 31, 2013
Write 0.00000000012 in Scientific Notation
Suppose the distance from Earth to Planet-X is 4,502,233,434,224,445,657,213,455,467,634,345,654,634,234,333,345,547,665,754,234,647,673,535,345 light years away and you needed to write that distance 20 times in various places in a book report. Wouldn't it be nice if there was a way to "abbreviate" it? Scientific notation is how we can write numbers in a "shorter" way. In this case we could round the number to say 4,500,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, but we'd still have deal with all of those zeros. Using scientific notation we could write the distance as "approximately 4.5 x 10^72" and capture the size of the number without needing to write all of its digits. Here is how it works:


So... 0.00000000012 = 1.2x10^-10
Friday, March 29, 2013
Limit Definition of Derivatives
Use the definition of derivatives to find the derivative of sqrt(x)
Solution:
Multiplying by a conjugate can be a useful strategy and it helps in this problem. We also notice that sqrt(2) is only defined for real numbers greater than or equal to 0 (for calculus). This means the absolute value of an expression is also greater than or equal to 0. In the denominator we must be careful not to multiply because factoring out the delta-x is easier.
Solution:
Multiplying by a conjugate can be a useful strategy and it helps in this problem. We also notice that sqrt(2) is only defined for real numbers greater than or equal to 0 (for calculus). This means the absolute value of an expression is also greater than or equal to 0. In the denominator we must be careful not to multiply because factoring out the delta-x is easier.
Tuesday, March 26, 2013
Factoring a degree 4 polynomial
Factoring polynomials is as much an art as it is a skill and we can get better with practice. It helps to know some important facts about them to make our work easier. For instance, if all the coefficients are real and we are factoring over the real numbers, we'll always be able to factor down to degree 1 or degree 2 polynomials. We can "cheat" by graphing the polynomial and checking when it crosses the x-axis. And we can "cheat" by using a bunch of tools from Pre-Calculus topics: Descartes' Rule of signs, synthetic division, etc. Finally there is the option of using software on a calculator, computer, or the internet. Then going back to another strategy with the foreknowledge of the actual solution (shameful).
Here we employ a couple of handy strategies. Grouping is our most important tool and we exploit it ruthlessly. Next we notice that if we replace 7x^2 with 5x^2 + 2x^2 (on line 2 of the solution) we get two polynomials that can be factored - each with a common factor of x+1. On line six we use the same strategy by writing 5x^2 as 2x^2+3x^2
Here we employ a couple of handy strategies. Grouping is our most important tool and we exploit it ruthlessly. Next we notice that if we replace 7x^2 with 5x^2 + 2x^2 (on line 2 of the solution) we get two polynomials that can be factored - each with a common factor of x+1. On line six we use the same strategy by writing 5x^2 as 2x^2+3x^2
Sunday, March 24, 2013
Saturday, March 23, 2013
Limit of a sequence
Limit of a sequence. We us the handy strategy of re-writing the limit in a more convenient way that does not change it's value. And by using the conjugate of the expression, we are able so simplify. Alternately we can apply the direct comparison test. 1/n is a sequence that we know converges, so we compare our sequence to it. After some algebra, we can see that the inequality will hold.
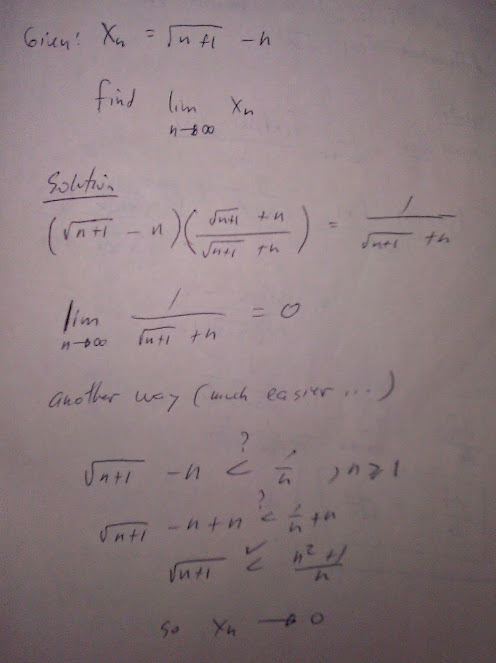
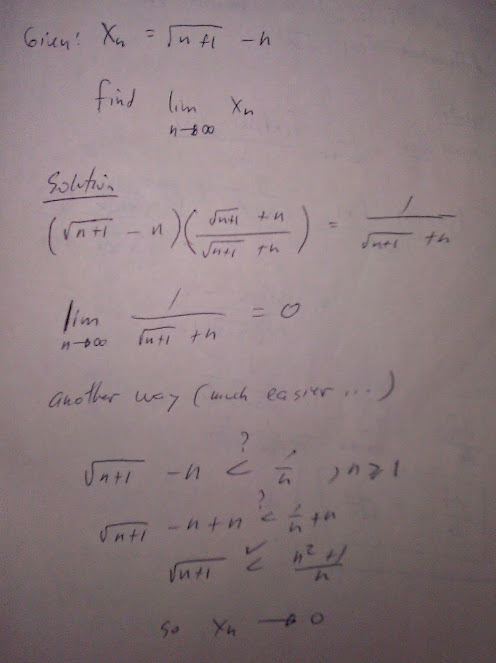
Bearings
The direction to an object is described as the number of degrees east or west of north or south.
A is read "30 degrees East of North"
B is "60 degrees West of North"
C is "70 degrees East of South"
D is "80 degrees West of South"
Thursday, March 21, 2013
Derive Area Formula for a Trapezoid
Use Triangles to derive the formula for a trapezoid
So we denote the trapezoid area as A-sub-T and subtract the area of the small triangle on top from the entire triangle. We can also use the idea of similar triangles to replace parameters from the top triangle.
Finally we rename h-sub-2 as h so that it looks more familiar.
first post...
This is my first post of my "first blog". The actual first blog was somewhat of an experiment. It's called "What's This Blogging all about?" and I used it to learn how to set up a blog. I think I'll keep it and use it for something...
So this blog will be where I post examples of math problems that I've worked out. I'm sure it wont be great at first, but I hope to get good, fast.
So this blog will be where I post examples of math problems that I've worked out. I'm sure it wont be great at first, but I hope to get good, fast.
Subscribe to:
Comments (Atom)